MODELAREA MATEMATICA LA INCEPUTUL NOULUI MILENIU SI IMPORTANTA EI PENTRU INVATAMÂNTUL SUPERIOR MILITAR

Lect.univ. DANIELA RACHITAN

    Abstract

    The present paper tries to explain the important role of mathematical modeling in the present society and in the army this millenium. Due to sureveillance systems which can continuously trace the enemy, there is a need for numerous forces to neutralize it; the basic tactics of the new millenium being modeling and simulation. Besides emphasizing the main types of models and their fields of applicability. The implementation of mathematical modeling and simulation started by providing the different compartments of the military organization with performant computers and well trained personnel. We can not achieve the desired performances unless we take into accent the mathematical modeling (we refer first of all to the military education system with all its stages).

    Este esential a intelege ca in societatea actuala deci si in armata moderna a acestui mileniu, modelarea matematica reprezinta o necesitate care isi cere drepturile. Astfel, Wilhem Westmoreland afirma „pe teatrul de operatiuni al viitorului fortele inamice vor fi localizate, urmarite si lovite aproape simultan datorita utilizarii modelelor matematice, legaturilor informatice si controlului automat al focului. Odata cu apropierea de certitudine a probabilitatilor de distrugere ale primei lovituri si datorita sistemelor de supraveghere care pot sa urmareasca continuu inamicul, nevoia de forte numeroase pentru a neutraliza rezistenta va fi mai putin importanta".

    1. Definitia modelului matematic
    Notiunea de model este strâns legata de matematica.
    G. Moisil mentiona „...pe lânga matematica metrica (clasica) s-a elaborat matematica structurala logica. Matematica moderna este o stiinta dominata de categoria structurii". Matematica are azi la baza algebra (stiinta discontinuului) si topologia (stiinta continuului), aceasta ca un raspuns la caracterul continuu si discontinuu al realitatii.
    In acceptiunea lui Bellman, dovada cunoasterii fenomenelor o constituie masura in care se reuseste prevederea desfasurarii lor, ori, aceasta necesita masuri cantitative a caror formule si precizare satisfacatoare implica folosirea unui model matematic.
    Definitia 1. Modelul matematic este o multime de una sau mai multe relatii matematice intre variabile (care reprezinta valori numerice) si una sau mai multe ipostaze admise privind desfasurarea fenomenului.
    Din aceasta definitie rezulta ca pentru a descrie matematic legile de aparitie si dezvoltare a unui fenomen este necesar sa se delimiteze laturile lui esentiale, cantitative, carora sa li se asocieze ansamblul relatiilor matematice adecvat fenomenului respectiv. In limbaj matematic, legatura diferitelor laturi ale fenomenului si dependenta calitativa si cantitativa a acesteia de factorii care il conditioneaza se exprima sub forma unor raporturi cantitative sau a unor relatii matematice intre marimile reprezentate de notatiile adoptate.
    Modelul matematic este un model realizat cu instrumente matematice a unei actiuni ce trebuie optimizata. Modelarea fenomenelor permite descoperirea si studiul aspectelor si proprietatilor mai profunde ale fenomenului reprezentând un sintetizator pentru trecut si un mobil de cercetare pentru viitor.
    Modelarea matematica opereaza cu marimi numerice fara a conditiona modul de interpretare subiectiva, intr-un anumit context a rezultatelor obtinute. Ea presupune cunoasterea tuturor elementelor care concura la descrierea fenomenului, posibilitatea exprimarii cantitative si pe cât posibil fara nici un adaos subiectiv, cunoasterea cât mai amanuntita a conditiilor in care are loc fenomenul, precizarea restrictiilor impuse unor marimi sau functii, precum si completa definire a scopului urmarit.
    Mircea Malita defineste modelul ca „o reprezentare mintala sau scrisa, calitativa sau matematica a unei parti dintr-o realitate ce constituie un sistem (adica un tot avându-se partile interconectate). Modelul selecteaza componentele cele mai reprezentative ale sistemului si descrie relatiile care se leaga". Crearea unui model nu serveste numai cunoasterii ci are si scopuri practice, constituind si o baza de experimentare.
    Toate fenomenele realitatii inconjuratoare se prezinta cercetarilor nu prin esenta lor in mod direct, ci printr-o multitudine de aspecte globale si locale. Este posibil, ca in matematica sa se dea o scriere generala a fiecarui fenomen, deci un model (matematic). Exprimarea cea mai generala posibila a aspectelor globale si locale ale fenomenelor, ca si interdependenta lor se pot face prin relatia generala:
    F (P,T) = G (P,T) + L (P,T) (1)
    care reprezinta un model formal, logic al fenomenului. Aici P si T sunt coordonatele partiale temporale ale fenomenului, iar functiile G si L redau tendintele globale (determinante), respectiv locale (aleatoare).
    In masura in care evidentiaza in mod corect o proprietate a fenomenului, modelul reprezinta un rezultat, reflecta o legatura, sintetizeaza legi din realitate, deci este un adevar obiectiv.

    2. Impactul social al modelelor matematice

    Impactul pe care modelarea matematica il are in gândirea oamenilor, in „gândirea" societatii, trebuie judecat in conjunctie cu impactul matematicii insasi si cel al calculatoarelor electronice. Toata lumea este de acord ca o trasatura definitorie a perioadei pe care o traim este spiritul stiintific care o domina. De multe ori, aceasta viziune stiintifica asupra lumii, aceasta continua formulare si rezolvare a problemelor, se confunda cu spiritul matematic.
    Despre rolul si locul matematicii in configuratia culturii contemporane nu este nevoie sa mai vorbim. Pe de alta parte calculatoarele, masele plastice si reactiile nucleare controlate isi dispusa in multe opinii locul intâi intre cele mai importante descoperiri ale secolului nostru care numai de descoperiri nu duce lipsa. In legatura cu relatia dintre calculatoare, modele si societate retinem ideea „practic, nu exista domeniu de activitate in care sa nu fi patruns metodele cibernetice, si odata cu ele calculatorul. Dar calculatorul este in fond un model. Cele analogice sunt modele – de obicei – electronice ale unor relatii matematice, iar cele digitale modele ale unor algoritmi. Tocmai aceasta face ca in momentul de fata sa existe un puternic interes atât pentru calculatoare, cât si pentru modele si pentru teoria generala a modelelor".
    In aceasta companie selecta modelarea matematica, aflata la intersectia celor doua mari domenii amintite – matematica si calculatoarele isi imparte gloria si reprosurile cu ele, de multe ori nefiind prezenta la „festivitati".
    Rolul social al modelelor matematice este insa extrem de mare, chiar imposibil de evaluat. Activitatea de conducere economica este de neconceput fara modele matematice; ele sunt utilizate in studiul operelor literare, in previziuni privind evolutia vremii, zborurile cosmice. Desigur ca modelele matematice sunt folosite si in activitatile militare pentru ridicarea capacitatii de lupta, intarirea ordinii si disciplinei militare, executarea actiunilor de lupta.
    Rezultatele obtinute in toate aceste domenii incurajeaza uneori pâna la entuziasm, folosirea modelelor. Din fericire, entuziasmul fara acoperire este invariabil contracarat de experienta practica. Asa cum am vazut, exista lucruri „care nu se pot face", care nu se pot face in principiu, sau nu se pot face cu resurse date. Matematica isi descopera si jaloneaza ea insasi propriile limite. In interiorul acestor limite, credem ca entuziasmul nu trebuie cenzurat.
    Modelarea matematica a dat si va mai da inca multe rezultate de mare utilitate.

    3. Cerinte ale modelului matematic

    Pentru a fi admis, modelul matematic trebuie sa satisfaca câteva cerinte impuse atât de practica modelarii cât si de utilizarea lui.
    In primul rând modelul matematic va asigura o redare aproximativa a fenomenului modelat. Aceasta inseamna ca esenta reflectata de model prin structura sa fie cât mai apropiata de esenta continutul obiectiv al fenomenului real. Cu cât se abate mai putin de la fenomen, cu atât mai corecte se dovedesc datele furnizate de model, deci si deciziile luate pe baza lor.
    In al doilea rând se impune ca modelul sa exprime clar, precis si realist scopurile propuse, sa fie riguros. Prin urmare functiile care descriu scopurile (ale caror extreme minime sau maxime se cauta) este necesar sa dea o exprimare matematica cât mai exacta a lor, sa fie simple ca expresie (pentru a asigura o prelucrare mai usoara) si sa cuprinda cele mai importante variabile ale problemei.
    Contradictie fundamentala a modelului consta in aceea ca el nu coincide cu scopul propus, dar serveste la cunoasterea acestuia, cunoastere care intotdeauna se obtine la prima varianta, ci de regula, prin perfectionarea permanenta a modelului, prin negarea dialectica a unui model de catre altul.
    Un model este valabil numai pentru laturile realitatii pe care le reflecta, valoarea lui apreciindu-se dupa ceea ce exprima el si nu dupa ceea ce ar trebui sa exprime un model ideal.
    O alta cerinta pe care trebuie sa o satisfaca un model matematic este ca intr-o structura relativ simpla si de mica intindere sa fie cuprinse cât mai multe din interconexiunile diverselor aspecte ale fenomenului. Aceasta inseamna ca având in structura sa cât mai putine restrictii, modelul sa exprime cât mai multe din proprietatile fenomenului.
    La ora actuala exista o clasa bogata de algoritmi care asigura tratarea la nivel corespunzator a majoritatii problemelor practicii din diferite domenii inclusiv a problemelor militare, iata de ce apare necesitatea studierii aprofundate a modelelor matematice.

    4. Tipuri de modele matematice

    Experienta practica acumulata prin realizarea unui numar mare de modele au aratat ca pentru acelasi model cerintele formulate formeaza un ansamblu contradictoriu. De aceea orice model matematic satisface, de regula, numai o parte a acestor cerinte.
    Functie de informatiile pe care le contin si le pot oferi, precum si al interpretarii rezultatelor obtinute pe baza lor, modelele se clasifica in doua mari grupe: deterministe si stohastice. Aceste modele sunt in strânsa legatura cu unele tipuri de decizie si anume cu deciziile certe si de risc.
    Modelul determinist se caracterizeaza prin aceea ca parametrii ce definesc procesul modelat sunt cunoscuti cu precizia necesara garantarii valabilitatii rezultatelor. Modelul nu are in structura sa nici un factor aleator (se poate observa usor similitudinea dintre modelul determinist si decizia certa).
    Variabilele de decizie (necunoscutele) ale modelului iau valori in domeniul restrictiilor impuse de structura modelului. Solutia obtinuta prin rezolvarea modelului satisface restrictiile (solutiile posibile) si corespunde criteriului optim adoptat. Aceasta solutie poarta si un caracter determinist.
    Modelul determinist se poate baza pe metodele algebrei liniare, pe teoria ecuatiilor diferentiale, teoria probabilitatilor, teoria jocurilor etc.
    Modelul stohastic se caracterizeaza prin parametri ce sunt variabile aleatoare ale caror valori nu pot fi inlocuite cu valorile medii corespunzatoare, fie pentru ca aceste valori medii nu sunt cunoscute, fie ca daca ar fi inlocuite cu valori medii, rezolvarea modelului ar putea conduce la solutii (decizii) neconforme cu realitatea (se poate observa legatura intre modelul stohastic si decizia de risc). In modelul stohastic variabilele aleatoare pot fi:

• cunoscute numai pentru unele variabile aleatoare, ceea ce este caracteristic pentru modelele cu incertitudini partiale;
• cunoscute toate, ceea ce genereaza „adevaratele" modele stohastice.

    De rezolvarea modelelor stohastice se ocupa programarea stohastica (rezultata din imbinarea teoriei probabilitatilor si proceselor aleatoare ca si a statisticii matematice cu teoria optimizarii).
    Modelele matematice mai pot fi clasificate functie de instrumentul matematic utilizat. Astfel, sunt modele ce utilizeaza cercetarea operationala (care cuprinde modele liniare, neliniare, modele de programare dinamica, modele ce folosesc teoria grafurilor); modele ce utilizeaza teoria jocurilor; modele ale teoriei deciziei; modele ale teoriei asteptarii; modele ce folosesc combinatorica; modele statistice; modele probabilistice; modele ce utilizeaza algebra; modele ce utilizeaza geometria, trigonometria si geometria analitica. In continuare voi incerca o descriere amanuntita a acestor tipuri de modele.
    Modele liniare sunt utilizate la analiza situatiilor economice, comerciale, militare când de obicei exista resurse deficitare (oameni, masini, armament) care trebuie folosite in asa fel incât sa realizeze cantitatile necesare de produse, aducându-se la valoarea optima unul sau mai multe scopuri (cheltuieli, venituri, pierderi ale inamicului, pierderi proprii, probabilitatea de descoperire, probabilitatea de distrugere etc.). In cazul programarii liniare de exemplu modelul este de forma:
     in conditiile  (2)

    Functia f(x) poate fi probabilitatea de indeplinire a misiunii, numarul mediu de purtatori nimiciti de contraactiunea inamica, rezultatul mediu al actiunii fortelor (mijloacelor) asupra obiectivelor inamice.
    Coeficientii pot avea interpretarile:

c_{j –} probabilitatea distrugerii mijlocului j de inamic; probabilitatea de nimicire a tintei j; intervalul de timp in care armamentul de tip j (sau subunitatea j) trebuie sa execute o misiune;
c_ij – probleme de transport (costuri, distante);
a_ij – numarul de lovituri de tip i aflate pe purtatorul j;
t_i – cantitatea totala de lovituri de tip i aflate la dispozitie la un moment dat. Metoda principala de rezolvare a acestei categorii de probleme este algoritmul simplex (cu toate variantele lui) care este legat foarte strâns de structura multimii solutiilor admisibile. Aceasta legatura il face sa fie deosebit de eficient. In plus, el este simplu si usor de programat pe calculator. Un caz particular de model liniar cu multe utilizari si in activitatile militare curente il constituie modelul activitatilor de transport (cu toate variantele cunoscute). Pentru el au fost elaborate metode specifice de rezolvare (metoda distributiva, metoda distributiva modificata, metoda acoperirii zerourilor, metoda potentialelor etc.) care tin seama de particularitatile structurii modelului (restrictiile sunt toate egalitati, coeficientii a_ij au toti valoarea 1 si toate solutiile – admisibile optime sunt numere intregi).

Modele neliniare sunt folosite in marea majoritate a actiunilor militare si s-au dezvoltat foarte mult odata cu introducerea metodei multiplicatorilor. Acestea au urmatoarea structura:

- sa se determine extremul functiei f(x) cu urmatoarele conditii: g_i(x){?, =,?} b_j, (i =1,..., n) unde x este (x_i,..., x_n); f o functie neliniara; g_i functii neliniare; b_j constante date. De aceste modele, de rezolvarea lor se ocupa programarea neliniara cu multiple aplicatii in domeniul militar, cum ar fi problema repartitiei loviturilor pe tinte.

Multe fenomene, procese ale naturii si domeniului militar au o evolutie care, pe planul gândirii poate fi conceputa ca având o desfasurare in etape, fara ca prin acesta sa se denatureze intr-o masura importanta esenta lor. Asa sunt, de exemplu, procesele de luare a deciziilor. Astfel de fenomene se trateaza matematic prin modele de programare dinamica. Spre deosebire de programarea liniara, ea nu cere ca problemele sa fie caracterizate de ecuatii de forma particulara. De aceea pentru programare dinamica nu exista un algoritm general, ceea ce face ca ea sa fie flexibila si sa ofere raspunsuri la situatii dificile, greu de rezolvat prin alte metode. Iata câteva exemple de probleme militare, care se pot rezolva prin programare dinamica:

• Problema incarcarii optime a mijloacelor de transport, cunoscând unitatea de incarcatura de fiecare tip de material si valorile corespunzatoare ale costului unitar de t/km. de transport, este formulata, astfel:

(3)

unde ?=(x₁,x₂,…,x_m), se cere 

cu conditiile:

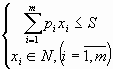(4)

unde: f_m (S) - costul incarcaturii;

S – capacitatea de incarcare;

c_i – costul incarcaturii de tip i;

p_i – masa incarcaturii de tip i;

x_i – cantitatea incarcaturii de tip i;

N – multimea numerelor naturale.

• Problema repartizarii a „m" mijloace de foc pe „n" obiective in scopul realizarii unor distrugeri cât mai mari, cunoscând ca fiecare obiectiv este caracterizat de un grad de distrugere anumit si ca fiecare mijloc nimiceste un obiectiv de tip „i" cu probabilitatea p_i = 1 – exp. (- a_i x), i se asociaza modelul matematic urmator:

f_k+1(x_k+1) = max {A_k+2 [1- exp (- a_k+2 (x_k+1 – x_k ))] + A_k+3 [1- exp (- a_k+3 x_k)]} (5)

unde:

f_k+1(x_k+1) - reprezinta avariile maxime provocate inamicului;

A_k+2, A_k+3 - efectul unei rachete asupra obiectivului cu numarul k;

a_k+2, a_k+3 - coeficientii ce caracterizeaza mijlocul de lupta respectiv.

• Problema repartizarii mijloacelor de lupta intre unitati in actiunile ce se desfasoara in mai multe etape, cunoscând totalul L de mijloace ce trebuie sa se repartizez pe doua unitati in cantitatile g_i , (i=1,...,n). Cunoscând ca eficienta oricarei unitati este data de valoarea functiilor g si h si ca numarul de etape este n, se obtine urmatoarea ecuatie functionala:

f_n (x₀, y₀, y₁ ,...,y_n-1) = g (y₀ ) + h (x₀ – y₀ ) + ...+ g (y_n+1) + h (x_n-1 – y_n-1) (6)

unde:

n₁, n₂, ..., n - reprezinta valorile repartitiei;

f – eficienta totala a mijloacelor de lupta repartizate;

g – eficacitatea primelor unitatii repartizate;

h – eficacitatea celorlalte unitati repartizate.

Modelele ce folosesc teoria grafurilor sunt utilizate in domeniul militar pentru optimizarea transporturilor pe reteaua rutiera, alegerea celor mai bune (scurte) itinerare pentru deplasarea unor forte dintr-un raion intr-altul, optimizarea pregatirii rachetelor la punctele tehnice, planificarea optima a realizarii unor lucrari (tehnice, genistice, de mascare etc), atingerea celor mai bune itinerare pentru trecerea printr-o retea de drumuri si pase de navigatie.

Desi veche ca problematica, teoria grafurilor a fost relansata in actualitate mai ales odata cu aparitia metodelor de tip PERT si a constituirii teoriei retelelor. S-a observat ca multe activitati, printre care si cele militare, pot fi modelate matematic cu multa eficienta, folosind o structura de graf imbogatita cu o serie de functii asociate.

Situatiile conflictuale specifice domeniului militar au generat o clasa foarte importanta de modele matematice – modelele teoriei jocurilor. Deoarece in probleme cu mai multi parteneri si de dimensiuni, incercarile de optimizare nu sunt satisfacatoare, apelul la teoria jocurilor poate furniza solutii destul de bune, ea având rolul sa ordoneze dupa o multime data de criterii multimea variantelor obtinute prin variatia parametrilor. In principal teoria jocurilor cuprinde: elaborarea definitiei solutiei jocului; demonstrarea existentei solutiei; elaborarea metodelor de gasire a solutiilor; aspecte practice ale folosirii teoriei jocurilor. Desigur, aceasta teorie nu poate sa cuprinda in schemele ei toate situatiile reale, dar multe din ele pentru o experienta determinata se pot incadra intr-o schema de joc. Un joc este caracterizat prin numarul de participanti, actiunile lor posibile si repartitia câstigurilor in functie de comportarea lor.

In domeniul militar caracterizat prin situatii conflictuale teoria jocurilor si-a gasit un câmp larg de aplicare. Aceasta teorie s-a dovedit deosebit de utila in tratarea problemelor de cautare a tintelor submarine in care optimizarea probabilitatii de descoperire oferite de lanturile Markov neomogene este extrem de greoaie. Un exemplu de aplicare a teoriei jocurilor il constituie algoritmul propus de Juttler pentru rezolvarea problemelor de extrem multicriterial, foarte frecvent intâlnite in domeniul militar, deoarece analiza situatiilor militare pe baza unui singur criteriu de eficienta este departe de a satisface utilizatorul. Alte exemple de aplicare a teoriei jocurilor sunt: alegerea tipului de armament cu eficacitatea cea mai ridicata pentru lovirea unor obiective; alegerea procedeului tactic, a mascarii, urmaririi inamicului, etc.

Un alt tip de modele utilizate in domeniul militar sunt modelele ce folosesc combinatorica. Combinatorica are rolul de a imbogati problemele cu o serie de caracteristici numerice ce reflecta anumite proprietati profunde ale esentei fenomenelor. Putem mentiona o serie de problemele aplicative militare cu caracter combinatorial:

• amplasarea in câmpul de lupta a unor obiective care actioneaza la distanta (a statiilor de radiolocatie, a minelor);
• construirea codurilor pentru transmiterea informatiilor cu caracter secret;
• alegerea itinerariilor (gasirea celui mai scurt drum).

In problemele combinatoriale se cerceteaza multimi discrete, in general finite, atentie deosebita acordându-se la doua operatii alegerea unor submultimi si ordonarea elementelor.

Combinatorica are drept componente principale: probleme de numarare, existenta solutiilor, elaborarea algoritmilor de gasire a solutiilor si altele.

Modelele probabilistice reprezinta un alt tip de modele ce si-au dovedit utilitatea in mediul militar. Astfel, aceste modele sunt folosite pentru a realiza modele ale duelurilor de foc si ale luptei de grup, pentru determinarea rezultatului unei confruntari, a raportului de forte, pentru determinarea necesarului de forte si mijloace si optimizarea intrebuintarii fortelor.

In legatura permanenta modelele probabilistice sunt cu un alt tip de modele matematice care se utilizeaza in domeniul militar si anume modelele statistice. In continuare voi prezenta câteva exemple cu aplicatie in organizatia militara: estimarea eficacitatii unor sisteme de armament; studiul implicatiei pe care fenomenele politice si economice le au asupra evolutiei starilor conflictuale; estimarea parametrilor la tragere (punctul mediu, distantele de tragere); estimarea necesarului de materiale, forte si mijloace necesare unei anumite actiuni militare; prelucrarea datelor obtinute prin cercetare in scopul realizarii unor prognoze asupra desfasurarii crizelor (conflictelor).

Un alt tip de modele ce-si gaesc din ce in ce mai mult aplicatie la fenomenul militar sunt modelele teoriei asteparii. Teoria asteptarii mai este denumita si teoria deservirii in masa, principalele elemente ale unei probleme de asteptare fiind sursa, firul de asteptare, statia de serviciu. Teoria asteptarii rezolva probleme de genul: numarul de unitati din firul de asteptare la un moment A; numarul de unitati ce sunt servite la un moment A; timpul mediu de asteptare a unei unitati in fir. Teoria asteptarii rezolva probleme si cu specific militar cum ar fi: modelarea eficacitatii luptei individuale si de grup; repartizarea resurselor logistice, financiare pe unitati; repartizarea resurselor materiale functie de necesarul prognozat pe etape ale luptei etc.

Modelele ce utilizeaza teoria deciziei si-au dovedit in ultimul timp posibilitatea aplicarii eficiente in organizatia militara. Teoria deciziei are drept obiectiv modelarea structurii generale a procesului decizional. Teoria deciziei se ocupa de studiul jocurilor in care se actioneaza in conditii de incertitudine; adversarul in acest caz este natura, de aceea se mai numesc jocuri contra naturii.

Criteriile x₁, x₂,..., x_n pe care le are in vedere decidentul sunt de natura subiectiva depinzând de informatiile pe care le are despre el insusi. Având in vedere starea de incertitudine in care decidentul ia decizia exista uneori posibilitatea efectuarii unor experimente legate de jocul respectiv care pot ameliora rezultatul jocului in favoarea sa. Problema care se pune este legata de costul experimentelor (de timp, financiare etc.). De aceea putem considera 3 tipuri de jocuri contra naturii: jocuri fara experienta; jocuri statistice cu experienta unica; jocuri statistice cu esantionaj secvential. Toate aceste trei tipuri de jocuri pot fi folosite in domeniul militar pentru alegerea strategiei optime când avem mai multe optiuni, rezolvarea eficienta a jocurilor de razboi, luarea deciziei in munca de stat major.

Modelele ce utilizeaza algebra sunt foarte numeroase ele bazându-se in special pe elemente de calcul matricial, elemente ce stau la baza teoriei lanturilor Markov (utilizate eficient in problemele de duel) cât si pe teoria grupurilor si a corpurilor ce au aplicatii interesante in domeniul militar.

Si nu in ultimul rând mai sunt un tip de modele pe care le-am amintit in clasificare si anume modele ce utilizeaza geometria, trigonometria si geometria analitica. Aceste modele rezolva probleme legate de studiul proprietatilor traiectoriei, spatii periculoase, spatiul mort, spatiul defilat, determinarea unghiurilor de tragere, determinarea corectiilor, recalcularea abaterilor când directia de tragere face un unghi cu dimensiunea principala a tintei, rezolvarea unor probleme de topografie si topogeodezie.

Descrierea tipurilor de modele matematice prezentate mai sus vin sa sublinieze implicarea accentuata in ultimele decenii a modelarii matematice in domeniul militar in scopul optimizarii activitatilor specifice.

5. Calculatorul – instrument de modelare matematica

In prezent in prim planul progresului tehnic se afla dezvoltarea tehnicii informaticii adica a mijloacelor pentru stocarea, prelucrarea, transmiterea, pastrarea si folosirea informatiei. Cea mai mare materializare a acestui progres este elaborarea calculatorului electronic – mijloc tehnic universal pentru lucrul cu informatia.

Ritmul de dezvoltare a tehnicii de calcul este uluitor. Astfel, in ultimii 25 de ani viteza a crescut de 200 de ori si se dubleaza in medie la fiecare 2 ani. Dimensiunile calculatorului s-a redus de 10.000 ori. Acest calculator al mileniului al treilea nu mai este un obiect de lux ci a devenit un lucru comun. Acest lucru s-a intâmplat datorita faptului ca si-a dovedit utilitatea in diferite activitati, sporind eficienta deciziilor, scurtând timpul de executie si dând rezultate exacte si pertinente.

In ultimul timp, modelarea matematica a devenit oarecum sinonima cu folosirea calculatoarelor in abordarea diferitelor probleme. Evident este vorba de a o exagerare, calculatoarele pot face multe lucruri care nu sunt legate de modelare, iar in multe modele calculatoarele nu au nici o participare. Este insa un fapt real ca modelarea matematica foloseste in mod avantajos calculatorul.

Calculatorul impune limite in contradictie cu adecvarea, relevanta si pertinenta modelelor si solutiilor acestora. Astfel, „in fata constructorilor de modele matematice stau doua obiective contradictorii: modelul trebuie sa fie cât mai simplu de rezolvat si sa respecte cât mai precis situatia reala".

Interesanta pentru relevarea simbiozei tot mai pronuntate dintre modelare si calculator, e ca in ultima vreme pe lânga hardware (partea de echipament) si software (partea de programe), in limbajul legat de evolutia calculatoarelor si-a facut aparitia o noua categorie: fineware care ar reprezenta partea fina – instrumentele de modelare a proceselor din diferite tipuri de activitati.

Daca din punct de vedere hard calculatoarele puteau indeplini toate conditiile pentru a utiliza modele problema importanta era reprezentata de partea soft specifica modelarii. Acest obstacol a fost insa depasit pentru ca si cum se pot utiliza MATLAB si MATCAD – programe ce faciliteaza rezolvarea unor probleme ce presupun calcule dificile, ecuatii cu extreme, probleme de max si min, ecuatii diferentiale, integrale, analiza numerica.

In domeniul militar se utilizeaza un program specific de statistica SPSS capabil sa realizeze prelucrari statistice a datelor experimentale, usurând munca de determinare a parametrilor specifici modelarii matematice. Din acest motiv, el poate fi utilizat cu succes in modele de estimare, de studiere a eficientei unor procedee, arme sau in prelucrarea datelor legate de fortele de care dispune inamicul, amplasament etc.

Modelarea matematica prin calculator a realizat o strânsa legatura cu simularea ce a devenit procedeu de mare actualitate pentru instruirea trupelor.

Implementarea simularii si a modelarii a inceput prin dotarea diferitelor compartimente de la nivelul organizatiei militare cu calculatoare performante, s-a realizat o instruire a personalului pentru utilizarea calculatorului, a fost introdusa modelarea matematica ca disciplina de studiu in invatamântul militar.

Comandantul de subunitate beneficiaza de algoritmii si programele ce rezolva probleme de cercetare operationala, teoria grupurilor, programare liniara transpuse cu ajutorul QBASIC, TURBO PASCAL, C++ sau utilizând alte medii de programare, calculatorul asigurând aplicarea unor modele pentru rezolvarea unor probleme practice. Pentru a sublinia faptul ca modelarea este o componenta de baza in informatica militara, in anexa nr. 5 se prezinta coordonatele informaticii militare si domeniile de aplicatie a informatiilor militare.

Calculatorul este instrumentul de modelare pe care ofiterul poate si trebuie sa-l foloseasca in actiunile sale specifice, in luarea deciziei deoarece numai asa poate eficientiza demersul activitatii sale militare.