Aplicatii ale elementelor de statistica matematica
in domeniul artileristic

Lect.univ. Daniela Rachitan

    Necesitate si utilitate
    Fiecare dintre noi executa masuratori indiferent daca ne dam seama sau nu de acest lucru. Astfel, operatiunea de cântarire, de stabilire a temperaturii unui corp, obtinerea valorii numerice a unei lungimi sau a unui unghi, toate acestea sunt de fapt masurari.
    Ridicarea preciziei triangulatiei de stat, a lucrarilor cartografice si fotogrammetrice, presupune stabilirea de metode moderne privind prelucrarea rezultatelor obtinute din masurari.
    Problemele de baza, pe care le abordeaza teoretic si practic aceasta disciplina se pot formula in felul urmator:
-studierea legilor de repartitie a erorilor de masurare si determinarea criteriilor de estimare a preciziei masurarilor;
-stabilirea tolerantelor care ingradesc folosirea rezultatelor masurarilor in anumite limite de precizie date;
gasirea celei mai probabile valori a marimii determinate dupa rezultatele masurarilor multiple asupra ei;
-estimarea si calculul preliminar al preciziei, atât al masuratorilor (observatiilor) separate cât si al rezultatului lor final.
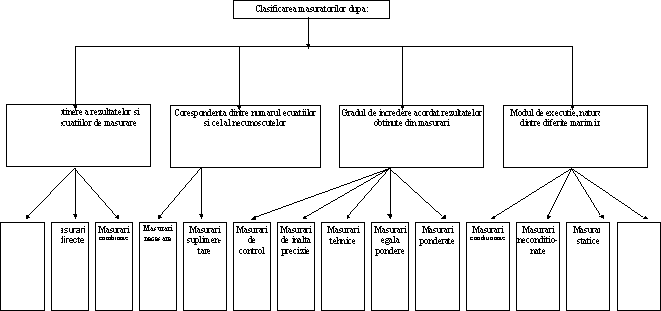
    In principiu, masurarile se clasifica dupa modul de obtinere a rezultatelor si aspectul ecuatiilor de masurare, corespondenta dintre numarul ecuatiilor si cel al necunoscutelor, precizia rezultatelor obtinute din masurari, complexul conditiilor de masurare, modul de executie a masuratorilor, natura si raportul dintre diferite marimi masurate (fig. 1).
    Elementele statisticii matematicii se folosesc si in tragerile artileriei nu numai in domeniul topogeodezic. Acestea sunt folosite pentru determinarea diferitelor abateri si erori.
    Aceste probleme ale abaterilor si erorilor sunt foarte mult tratate fiindca reprezinta unele din elementele principale ale tragerilor de artilerie pe baza carora putem trece la executarea tragerii de efect asupra obiectivului respectiv.

    Criterii de eliminare a valorilor necorespunzatoare dintr-un sir de rezultate obtinute din masuratori. Criteriul CHOUVENET, Criteriul SMIRNOV-GRUBBS, Criteriul ROMANOVSKI si Criteriul IRWIN
    In procesul de masurare, rebuturile pot aparea datorita mai multor cauze. Printre acestea pot fi mentionate urmatoarele:
-sirul de masuratori efectuat asupra uneia sau mai multor marimi fizice formeaza numai o parte din colectivitatea generala. Datorita acestui fapt oricând putem avea surpriza unui rezultat necorespunzator;
-in procesul masurarii, ca urmare a utilizarii unei metode de lucru necorespunzatoare sau datorita ignorarii surselor de erori sistematice, pot aparea elemente perturbatoare care sa influenteze negativ citirile efectuate la aparatele de masura.

    Eliminarea sau mentinerea unui rezultat din sirul de masuratori dat trebuie sa aiba la baza un criteriu stiintific.
    Consecintele unor operatii arbitrare pot afecta calitatea masuratorilor. Astfel, in ceea ce urmeaza vom mentiona câteva criterii de eliminare a valorilor necorespunzatoare din sirul de rezultate, fara insa a face consideratii asupra gradului de eficienta al fiecaruia dintre ele.

    2.1 Criteriul CHOUVENET

    Sa presupunem ca asupra marimii fizice s-au efectuat „n" masuratori, iar rezultatele x_iÎN(X,s ), unde i=1,n. Ordonând cele n rezultate in sens crescator sau descrescator:
x₁ <x₂<…<x_n
x₁ >x₂>…>x_n (1)
putem calcula media aritmetica () si abaterea medie patratica (S).

    Se elimina din seria de n masuratori o valoare x_i(i=1,n) a carei probabilitate de a iesi in afara limitelor intervalului maxim admis este .

    Pentru a determina limitele intervalului maxim admis(e ), in interiorul caruia dispersia valorilor observate in jurul mediei aritmetice este considerata normala, vom avea:

     (2)

unde t_q reprezinta abaterea maxima admisa de la media aritmetica (limita intervalului admis) exprimata in abateri medii patratice (S).

(3)

    Pe baza rezultatelor obtinute, criteriul CHOUVENET este definit de relatia:

(4)

    Pentru cazul extrem relatia (4) devine:

(5)

    Deoarece cunoastem probabilitatea  si cautam sa determinam limitele intervalului admis pentru o observatie (e ) este necesar sa cunoastem argumentul functiei F (t_q) pe care-l vom deduce din relatia (5):

(6)

care se extrage din anexa 3.
    Cu ajutorul formulei (6) putem hotari daca valoarea suspecta poate fi eliminata din sirul rezultatelor obtinute si vom proceda astfel:
    Calculam media aritmetica () si abaterea medie patratica (S) in raport cu toate rezultatele masuratorilor. Daca valoarea x_i este mai mare decât toate celelalte i-1 valori, vom aplica:

(7)

    Rezultatul calculat va fi comparat cu valoarea suspecta x_i. Daca x_c>x_i, atunci valoarea suspecta se mentine in sirul dat ca fiind corespunzatoare ; in caz contrar aceasta valoare trebuie interpretata ca o eroare grosolana si eliminata din sir.
    In ipoteza ca valoarea suspecta x_i este mai mica decât toate celelalte valori ale sirului de masuratori, aplicam relatia:

(8)

    Astfel, daca valoarea suspecta x_i a unui sir de rezultate obtinute din masuratori este mai mare decât valoarea calculata x_c, se accepta ipoteza ca masuratoarea este necorespunzatoare. Daca valoarea suspecta x_i este mai mica decât x_c, ea se elimina din sirul dat.
    In practica sunt cazuri când, dupa ce o valoare a fost eliminata conform criteriului CHOUVENET, o alta valoare din sir, diferita fata de celelalte valori pare suspecta. In acest caz noul rezultat va fi supus criteriului CHOUVENET, tinând seama ca cel eliminat nu mai este o valoare a sirului si ca noua medie se calculeaza numai cu rezultatele ramase. Acest procedeu se continua pâna ce constatam ca nici un rezultat nu iese in afara limitei de toleranta admisa.
    In sfârsit, este locul sa amintim ca nu intotdeauna eliminarea unui rezultat dintr-un sir dat este o consecinta a aparitiei unei greseli. Sunt situatii când anumite rezultate se elimina pentru simplul motiv ca valoare medie obtinuta fara aceasta se presupune a fi mai apropiata de valoarea adevarata.

    2.2 Regula lui CHARLIER

    Pentru stabilirea formulei se pleaca de la conditia:

(9)

care in caz extrem devine 

de unde rezulta ca  (10.4)

    De aici putem calcula marimea t_q fata de care trebuie hotarât daca valoarea suspecta x_m se mentine sau nu in sirul de rezultate considerat.
    Comparând relatia (6) cu (10) constatam ca acestea difera. Cu alte cuvinte, probabilitatea ca eroarea sa depaseasca limitele de toleranta stabilite de CHARLIER este de doua ori mai mare decât probabilitatea ca aceeasi eroare sa depaseasca limitele de toleranta stabilite de CHOUVENET.

Exercitiul (1):
Efectuându-se 20 masuratori a unei distante cu ajutorul unui aparat de masura s-au obtinut valorile din tabelul 1.
Se cere, folosind criteriul CHOUVENET sau CHARLIER, sa se arate daca valoarea x_min din sirul de masuratori considerat trebuie sau nu eliminata.
Tabelul 1

Nr. crt.	xi	ni	xini			ni	Formule si rezultate
1	2	3	4	5	6	7	8
1	16,88	1	16,88	+0,08	0,0064	0,0064
2	16,86	1	16,86	+0,06	0,0036	0,0036
3	16,85	1	16,85	+0,05	0,0025	0,0025
4	16,84	1	16,84	+0,04	0,0016	0,0016
5	16,83	1	16,83	+0,03	0,0009	0,0009
6	16,82	5	84,10	+0,02	0,0004	0,0020
7	16,81	3	50,43	+0,01	0,0001	0,0003
8	16,80	2	33,60	0	0	0
9	16,79	1	16,79	-0,01	0,0001	0,0001
10	16,77	1	16,77	-0,03	0,0009	0,0009
11	16,76	1	16,76	-0,04	0,0016	0,0016
12	16,75	1	16,75	-0,05	0,0025	0,0025
13	16,57	1	16,57	-0,23	0,0529	0,0529
	218,33	20	336,03	-0,07	0,0735	0,0753

In acest caz avem:

Deoarece in ambele cazuri x_c>x_min, masuratoarea suspecta se elimina.

    2.3 Criteriul SMIRNOV-GRUBBS

    Presupunând ca si mai inainte ca in sirul de masuratori dat una din valori se abate mult spre stânga sau spre dreapta fata de celelalte valori vom avea relatiile:

(11)

    Daca se considera ca fiecare rezultat x_i din sirul de masuratori considerat este normal repartizat, atunci repartitia marimii va depinde de numarul de masuratori efectuat asupra marimii fizice considerate.
    Plecând de la acest considerent teoretic fundamentat de SMIRNOV-GRUBBS a calculat repartitia marimii „y" in functie de n si q, unde 0,01<q<0,10.
    Cunoscând marimile n si q, se poate oricând gasi un numar t_q pentru care sa fie satisfacuta relatia :
    P{y>t_q}=q (12.4)

    Marimile t_q sunt date in anexa 3, pentru q=0,05.
    Deoarece metodica de calcul este asemanatoare cu cea de la criteriul CHOUVENET in cele ce urmeaza ne vom limita la un exemplu numeric.
Exemplul (2):
    Efectuându-se 20 masuratori asupra unei marimi fizice s-au obtinut valorile din tabelul 2.
    Se cere sa se arate daca ultima masuratoare din sirul dat trebuie sau nu eliminata, considerând drept nivel de semnificatie marimea q=0,05.
Tabelul 2

Nr. crt.	xi			Formule si rezultate
1	2	3	4	5
1	2,48	-1,46	2,132
2	2,75	-1,19	1,416
3	2,81	-1,13	1,277
4	2,95	-0,99	0,980
5	3,11	-0,83	0,689
6	3,26	-0,68	0,462
7	3,27	-0,67	0,449
8	3,43	-0,51	0,260
9	3,68	-0,26	0,068
10	3,78	-0,16	0,026
11	4,08	+0,14	0,020
12	4,15	+0,21	0,044
13	4,43	+0,49	0,240
14	4,49	+0,55	0,303
15	4,51	+0,57	0,325
16	4,55	+0,71	0,504
17	4,76	+0,82	0,672
18	4,84	+0,90	0,810
19	5,08	+1,14	1,300
20	6,35	+2,41	5,808
	78,86	+0,06	17,789

    2.4 Criteriul ROMANOVSKI

    Sa presupunem ca asupra unei marimi fizice a carei valoare adevarata nu este cunoscuta s-au efectuat „n" masuratori de egala precizie, iar rezultatele X_{i (i=1,n)} contin o valoare suspecta. In acest caz abaterea medie patratica de selectie va fi calculata numai din celelalte rezultate, urmând ca valoarea suspecta sa fie pusa sub semnul intrebarii, adica:

conform relatiei (12)

    Eroarea medie patratica S’ a intregului sir de masuratori poate fi exprimata prin intermediul marimii „S" folosind relatia aproximativa:

(13)

    In continuare vom arata urmatoarea fractie:

(14)

unde l este un numar pozitiv arbitrar de mic. Deoarece variabila intâmplatoare Z_c are o repartitie normala, probabilitatea ca | sa fie egala sau mai mica decât l se calculeaza cu ajutorul relatiei:
P{|£l }=p
    De altfel, datorita ultimului considerent enuntat, probabilitatea calculata se refera atât la x_max cât si la x_min.
    Pentru un „n" dat si q=0,05, marimea t_q se extrage din anexa 3. Aceasta marime se comporta ca cea calculata folosind relatia (14).
    Daca Z_c>t_q, atunci valoarea suspecta se elimina din sir ca fiind necorespunzatoare; in caz contrar, nu avem temei sa eliminam aceasta valoare din sirul rezultatelor obtinute din masuratori.
Exemplul (3):
    Aplicând criteriul ROMANOVSKI, se cere sa se stabileasca daca ultima citire din exemplul precedent trebuie sau nu mentinuta in sirul considerat.
    Rezolvare:

    Pentru q=0,05 si n=20 din anexa 3, obtinem t_q=2,15.
    Deoarece Z_c>t_q rezulta ca valoarea x₂₀=6,35 trebuie eliminata din sirul de citiri ca fiind necorespunzatoare. La aceeasi concluzie am fi ajuns daca aplicam criteriul CHOUVENET.

    2.5 Criteriul IRWIN
    Pentru examinarea unei observatii suspecte continuta in sirul dat, se mai poate folosi un alt criteriu propus de I. IRWIN inca din 1925. Criteriul este cunoscut sub denumirea de criteriul l ; se bazeaza pe faptul ca rezultatele dubioase sunt reprezentate de primii sau ultimii termeni ai sirului de masuratori ordonat in sens crescator sau descrescator. In acest caz calculul marimii l se efectueaza cu ajutorul relatiei:

(15)

    Marimea l calculata se compara cu valoarea l_p extrasa din anexa 4. Daca l >l_p, rezultatul suspect se exclude din sirul de masuratori ca fiind necorespunzator, in caz contrar acest rezultat trebuie mentinut.
Exemplul (4):
    S-au executat zece masuratori (cântariri) ale unei incarcaturi dintr-un lot de incarcaturi. S-au obtinut urmatoarele diferente: 0,2; 0,4; 0,0; 0,9; 0,3; 0,1; 0,0; 0,2; 0,2; 0,1. Sa se arate daca valoarea suspecta 0,9 trebuie exclusa sau nu din sirul de probe ca fiind necorespunzatoare.
Tabelul 3

Nr. crt.	xi			Formule si rezultate
1	2	3	4	5
1	0,2	-0,04	0,0016
2	0,4	+0,16	0,0256
3	0,0	-0,24	0,0576
4	0,9	+0,66	0,4356
5	0,3	0,06	0,0036
6	0,1	-0,14	0,0196
7	0,0	-0,24	0,0576
8	0,2	-0,04	0,0016
9	0,2	-0,04	0,0016
10	0,1	-0,14	0,0196
	2,4	0	0,6240

    Din anexa 4 pentru P=0,95 si n=10, obtinem l_p=1,5.
    Deoarece l > l_p rezultatul 0,9% trebuie eliminat din sirul de masuratori.

    Verificarea statistica daca rezultatele observatiilor sunt independente si aleatoare
    Inainte de a trece la tratarea statistica corespunzatoare a rezultatelor masuratorilor, trebuie sa ne convingem daca ele constituie cu adevarat o selectie intâmplatoare si sunt independente.
    Pentru verificarea statistica a independentei rezultatelor se pot folosi mai multe teste statistice, cum sunt:
    testul medianei selectiei;
    testul seriilor „ascendente" si „descendente";
    testul patratelor diferentelor succesive.

    Ultimele criterii evidentiaza mai puternic independenta rezultatelor masuratorilor si din acest motiv se prezinta dezvoltat in continuare.

    3.1 Testul patratelor diferentelor succesive

    Daca selectia pe care o analizam x₁, x₂, …, x_n a fost extrasa dintr-o populatie, judecam caracterul sau aleator pe baza acestui criteriu (ipoteza alternativa ar fi eventualitatea unei deviatii sistematice de la medie)
    Ori, in cazul masurarii distantelor cu aparatura electromagnetica, ne putem astepta la asemenea deviatii de la medie având in vedere in special o serie de influente ale factorilor externi si unele influente perturbatoare datorate regimului de lucru al aparatului.
    Pentru a verifica independenta rezultatelor observatiilor cu ajutorul acestui criteriu, se cerceteaza daca:

(16)

    Daca aceasta inegalitate este satisfacuta, ipoteza independentei rezultatelor marimii trebuie respinsa. Valorile pentru n<20 si pentru valorile cele mai uzuale ale nivelului de semnificatie a sunt date in urmatorul tabel.
    Tabel cu valorile  pentru n<20, a =0,05 si a =20,01.
Tabelul 4

N a	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
0,05	0,390	0,410	0,445	0,468	0,491	0,512	0,512	0,548	0,564	0,578	0,591	0,603	0,614	0,624	0,633
20,01	0,313	0,269	0,281	0,307	0,331	0,354	0,354	0,396	0,414	0,431	0,447	0,461	0,475	0,487	0,499

Valoarea g (n) se determina din formula:

(17)

unde:

(17p)

Exemplul (5):
Testul patratelor diferentelor succesive pentru g_0,05^min(18)=0,633
Datele sunt prezentate in tabelul 5.
Tabelul 5

Nr. mas.	Valorile distantei masurate	vi=xi-	vi2	di=vi+1-vi	di2
1	2	3	4	5	6	7	8	9	10
1	641,6	-43,6	1900,96	+10,2	104,04
2	651,8	-33,4	1115,56	-9,1	82,81
3	642,7	-42,5	1806,25	+22,3	497,29
4	665,0	-20,2	408,04	+25,2	635,04
5	690,2	+5,0	25,00	+15,3	234,09
6	705,5	+20,3	412,09	-17,8	316,84
7	687,7	+2,5	6,25	+10,4	108,16
8	698,1	+12,9	166,41	-10,5	110,25
9	687,6	+2,4	5,76	+0,1	0,01
10	687,7	+2,5	6,25	+24,7	610,09
11	712,4	+27,2	739,84	-27,7	712,89
12	685,7	+0,5	0,25	+13,6	184,96
13	699,3	+14,1	198,81	+6,3	39,69
14	705,6	+20,4	416,16	-9,3	86,49
15	696,3	+11,1	123,21	+0,1	0,01
16	696,5	+11,3	127,69	-4,9	24,01
17	691,6	+6,4	40,96	-3,3	10,89
18	688,3	+3,1	9,61	-	-
	=685,2		7509,10		3757,56	110,52	441,71	0,250	DA

    Indicatii asupra tendintei sistematice in rezultatele observatiilor se pot obtine si printr-o reprezentare grafica a abaterilor de la medie, cum rezulta din grafic in care am folosit datele din tabelul 5.

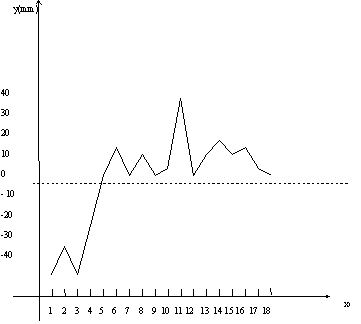
Fig. 2.

    Verificarea omogenitatii observatiilor

    Masurarea unei marimi se executa adesea pe parti, distingându-se unele de altele dupa timpul de executie, etc. In asemenea cazuri se pune problema daca aceste diferente de timp n-au influentat asupra rezultatelor observatiilor, care sa nu ne permita sa reunim cele doua parti pentru a forma o selectie comuna pe care sa o consideram drept selectie omogena extrasa din aceeasi populatie.
    In cazul masurarii de distante cu aparate electromagnetice, putem considera ca parti de selectie urmatoarele:
    rezultatele masurarii distantei in diferite zile cu acelasi aparat;
    rezultatele masurarii distantei cu aparate diferite dar cu acelasi ordin de precizie. Pentru verificarea propusa vom folosi
    rezultatele masurarii facute asupra distantei in zile diferite, cu acelasi aparat. In acest scop vom aplica testul T al lui STUDENT.

    4.1 Testul (T) STUDENT de verificare a omogenitatii a doua selectii

    Acest test se recomanda pentru realizarea sa practica, simpla. El presupune ca cele doua selectii sunt extrase dintr-o populatie:
    Având doua selectii:

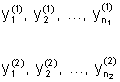(18)     Se pune problema daca cele doua solutii se pot considera omogene. Raspunsul la aceasta chestiune depinde de marimea: (19)

unde: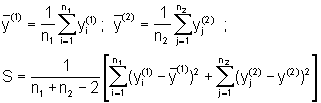 

    Daca rezulta ca

(20) se emite ipoteza omogenitatii selectiilor analizate.
    Pentru nivelul de semnificatie a si volumele selectiei n₁ si n₂ se gaseste in tabelul 6 punctul ta_/2(n₁+n₂-2) este procent 100 a /2 al distributiei t a lui STUDENT cu (n₁+n₂-2) grade de libertate.
TESTUL (T) al lui STUDENT pentru verificarea omogenitatii seriilor de masurari.
Tabelul 6

Gr.	Valorile masurate (partea variabila) pe grupa		Valorile „V" pe grupe		Suma valori-lor "V2" pe grupe
	641,6		-32,9		1082,41
	651,8		-22,7		515,29
	642,7		-31,8		1011,24
I	665,0		-9,5		90,25
	690,2		+15,7		246,49
	705,5		+31,0		961,00
		687,7		+13,2		174,24
		698,1		+23,6		556,96
		687,6		+13,1		171,61
						4809,49
		687,7		-8,2		67,24
		712,4		+16,5		272,25
		685,7		-10,2		104,04
		699,3		+3,4		11,56
II		705,6		+3,7		94,09
		696,3		+0,4		0,16
		696,5		+0,6		0,36
		691,6		-4,3		18,49
		688,3		-7,6		57,76
						625,95		339,71		18,43		0,47		8,66		-21,40		-2,47		-

< 
2,47>2,12

    Când ne referim la metodele de verificare a normalitatii unei distributii, trebuie sa distingem urmatoarele cazuri:
-când se dispune de un numar suficient de mare de observatii (de ordinul câtorva zeci); in acest caz verificarea normalitatii se face cu ajutorul criteriului hi-patrat, acesta fiind un caz rar in practica;
-când se dispune de un numar redus de observatii (de la câteva unitati la 10-30); in acest caz se vor folosi metode aproximative: metoda grafica sau metoda cu folosirea caracteristicilor empirice ale asimetriei si excesului;
-cazul in care se dispune de date care se refera la variabile aleatoare bidimensionale; se pot folosi atât caracteristicile empirice ale asimetriei si excesului, cât si metoda compararii frecventelor cu probabilitatile pe intervale de grupare.

Bibliografie
[1] Col. Iatan Alexandru, col. Purcarea Horia, Teoria tragerilor artileriei terestre, vol. II, Bucuresti, Editura Militara, 1973.
[2] Col. Petre, Teoria tragerilor artileriei terestre. Exercitii aplicative, Bucuresti, Editura Militara, 1981.