Teoria Markov aplicata in unele situatii tactice

Col.conf.univ.dr. Vasile Dumitru
Lt.col.conf.univ.dr.ing. Gelu Alexandrescu

    Activitatile pe care le desfasoara statele majore ale U. (MU) de RAA in vederea organizarii si conducerii actiunilor de lupta sunt supuse unor factori aleatori in timp micsorând in acest fel precizia evaluarii unor date ce stau la baza luarii unor decizii si, in consecinta, valoarea rezultatelor ce se obtin nu mai poate fi in concordanta cu realitatea. Se impune deci luarea in considerare a acestor schimbari astfel incât sa se diminueze, pe cât este posibil actiunile acestor factori aleatori cu caracter perturbator. Printre modelele matematice ce se preteaza acestui scop sunt si cele cuprinse in teoria proceselor de tip Markov, deoarece ele permit descrierea fenomenelor supuse actiunii factorilor aleatori.
    Pentru intelegerea modului de aplicare a teoriei markoviene in domeniul luptei si operatiei desfasurate de sisteme militare complexe, vom defini urmatoarele sintagme:
- stare (Si) - situatia in care se afla un sistem determinata de structura sa, de conditiile exterioare etc. si definita prin anumite marimi sau parametri. Pentru fiecare sistem pot exista S_i , i = 1, ... , n stari in care poate trece acesta pe timpul procesului, din care "starea initiala" (S_o) existenta la inceputul procesului si "stari reversibile", respectiv starile in care trece sistemul ulterior. Daca sistemul trece intr-o stare din care nu mai poate trece in alta, atunci aceasta este denumita "stare absorbanta";
- probabilitate de stare (P_i) - probabilitatea ce reflecta posibilitatea sistemului de a se mentine intr-o anumita stare "i" (P_i , i = 1 , ... , n);
- probabilitatea de trecere (P_ij)- probabilitatea ce reflecta posibilitatea sistemului de a trece dintr-o stare in alta pe timpul procesului, respectiv din starea "i" in starea "j". Aceasta probabilitate nu se determina in cadrul proceselor cu evolutie continua, deoarece pentru un anumit moment determinat acestea sunt nule (la fel ca si probabilitatile oricarei valori individuale ale functiei continuue a unei marimi aleatoare);
- densitatea probabilitatilor de trecere (l_ij) - este caracteristica proceselor continui si reprezinta limita raportului dintre probabilitatile de trecere P_ij ale sistemului in intervalul de timp Dt din starea S_i in starea S_j raportate la acest interval, adica: , unde:

· P_ij(D t) reprezinta probabilitatea ca sistemul aflat in momentul t in starea S_i, sa treaca din aceasta in starea S_j, in intervalul de timp Dt.
    Densitatile probabilitatilor de trecere se determina numai pentru starile la care j ¹ i.
    Pentru un interval foarte mic putem considera P_ij (D t)»l_ij(D t). Daca densitatea probabilitatii de trecere (l_ij) nu depinde de timp (adica in ce moment incepe intervalul D t), atunci procesul markovian se numeste omogen si neomogen in caz contrar.
- matricea de trecere este o matrice patratica "n x n" asociata lantului Markov care reprezinta multimea valorilor variabilei "densitatea probabilitatilor de trecere - l_ij", in care "i" reprezinta rândurile matricei, iar "j" coloanele acesteia, unde i si j iau valori de la 1 la n.
- graful starilor sistemului - graful asociat lantului Markov, la care nodurile (vârfurile) sunt caracterizate de starile sistemului, iar arcele de sensul de trecere dintr-o stare in alta. Pe fiecare arc se marcheaza densitatea probabilitatilor de trecere din starea "i" in starea "j" (l_ij).
    Graful este o pereche de multimi (S, U) si o aplicatie G: S_i ®l (S_i), astfel incât l(S_i) este multimea partilor S cu proprietatea G (x)Îl (Si), respectiv U={S_i, l ( S_i)½ S_iÎS}, unde:
· S - multimea vârfurilor grafului asociat lantului Markov, respectiv multimea starilor sistemului;
· U - multimea arcelor grafului (pentru lantul de tip Markov avem in vedere numai arce orientate ).
Ca urmare, fiecarei stare S_i i se va asocia o alta stare (sau o multime de stari) dupa schema: ,
adica lui S_i i se vor asocia numai acele stari pentru care exista o sansa ca sistemul sa ajunga din Si in aceste stari (este posibila trecerea).
    Daca lantul este omogen, graful asociat este unic. Lantului neomogen i se pot asocia un sir de grafuri corespunzatoare sirului de matrice de trecere asociate.
    Schema generala de reprezentare a unui graf asociat unui lant Markov este prezentata in fig. 1. Daca situatia conflictuala are caracter de "duel", in special in lupta aeriana, pentru respingerea sau cucerirea suprematiei aeriene etc., atunci graful are caracteristici
"absorbante".

         Lantul Markov asociat unei mari unitati de artilerie si rachete antiaeriene care se gaseste pe timpul unei confruntari directe cu inamicul aerian, se construieste tinându-se seama de urmatoarele conditii:
- S1 = marea unitate are capacitatea de lupta completa, respectiv atacul inamicului aerian nu a afectat structura organizatorica si functionala a acesteia;
- S2 = marea unitate are capacitatea de lupta diminuata ca urmare a dezorganizarii partiale a structurii sistemului de foc antiaerian, dar are un potential de lupta suficient de puternic ce ii permite sa-si continue misiunea;
- S3 = marea unitate are pierderi importante (pâna la 50 %) in mijloace principale de lupta, iar legaturile sunt dezorganizate si, ca urmare, sistemul de foc antiaerian este, in ansamblul sau, complet dezorganizat si, in consecinta, capacitatea de lupta este foarte slaba;
- S 4 = marea unitate este nimicita, respectiv scoasa complet din lupta.
    Ansamblul de probabilitati (p_n(i), i = 1, ..., n) poate fi reprezentat sub forma matriceala, in care numarul de elemente este dat de vectorul starilor posibile. Matricea va fi stohastica cu elemente care indeplinesc conditia de nenegativitate.
    Exemplul 1. In confruntarea aerian-antiaerian inamicul poate actiona in 5 variante, iar M.U. de riposta in 4, in urma carora valorile capacitatii de supravietuire a M.U. sunt cele din matricea de mai jos (coloanele semnifica variantele de atac, iar liniile variantele de riposta).

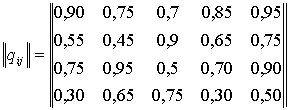
    Pentru a solutiona o asemenea situatie, initial se determina matricea probabilitatii de neutralizare a unitatii de riposta antiaeriana de catre aviatia adversarului:

1-=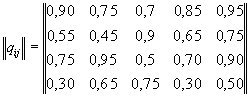

si apoi se determina matricea de trecere êêl_ijêêaplicând teoria probabilitatilor, având in vedere ca numarul total al evenimentelor este 20 (5 variante de atac si 4 variante de riposta). In urma calculelor matricea de trecere are structura:

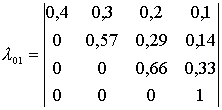, in care:

· rândurile reprezinta starile la momentul "n" (S₁, S₂, S₃, S₄) si coloanele starile la momentul "n + 1" (S₁, S₂, S₃, S₄).

    Matricea probabilitatilor de trecere se interpreteaza astfel:
- daca marea unitate a fost in starea S₁, atunci ea are 40 % sanse sa ramâna in aceeasi stare, 30% sa treaca in S₂, 20% in S3 si 10% in S4;
- daca marea unitate a fost in starea S₂, atunci ea nu poate trece in starea S1 (nu isi poate reface capacitatea de lupta), are 57% sanse sa ramâna in S2, 29% sa treaca in starea S3 si 14% in S4 etc.;
- se observa ca matricea este stohastica, iar trecerile sunt ireversibile. Ca urmare, graful asociat starilor sistemului, corespunzator situatiei de mai sus, poate fi reprezentat ca in variantele "a" si "b" din fig. 2.

    Pentru ducerea luptei (operatiei), in scopul stabilirii masurilor necesare, elaborarii deciziilor si, in special, a celor declansatoare de procese, executarii manevrei de forte si mijloace pentru constituirea structurilor etc., ne intereseaza ca dupa fiecare actiune posibila, in cazul nostru dupa fiecare atac, (lovitura) aerian(a), sa cunoastem probabilitatile de realizare a starilor posibile "i" = 1, ..., n.
    In acest sens, se alcatuieste sistemul ecuatiilor KOLMOGOROV - CHAPMAN corespunzatoare probabilitatilor de stare, sistem de ecuatii diferentiale ce au la baza graful starilor sistemului.
    Pentru rezolvarea sistemului se au in vedere si conditiile initiale (pentru t = 0), respectiv vectorul probabilitatilor de stare Po= (pi), i = 1, ..., n, ce reflecta probabilitatea de stare a tuturor starilor SiÎ S in momentul initial.
    Integrarea ecuatiilor sistemului conduce la obtinerea probabilitatilor de stare ca functii de timp, pentru care conditiile initiale se iau in raport de starea initiala a sistemului militar conflictual.
    In vederea rezolvarii sistemului de ecuatii diferentiale precizat anterior, oricare din cele patru ecuatii poate fi exprimata prin celelalte si, ca urmare, in final se vor obtine solutiile p₁(t), p₂(t), ..., p_n(t).
    Cu cât numarul starilor este mai mare, cu atât devine mai dificila rezolvarea sistemului, ceea ce impune utilizarea tehnicii de calcul.
    In continuare vom prezenta câteva situatii de aplicare rapida a "metodei lanturilor Markov" la sistemele militare conflictuale :
- analizând datele din exemplul anterior, respectiv matricea densitatii probabilitatilor de trecere, conditiile initiale [Po = (1, 0, 0, 0); t = 0 )] si modul de desfasurare a conflictului, rezulta ca:
- momentele la care au loc modificari in evolutia sistemului marii unitati de artilerie si rachete antiaeriene sunt, in mod firesc, momentele la care sunt executate tragerile antiaerene ca riposta la actiunea inamicului aerian; matricea densitatii probabilitatilor de trecere nu depinde de aceste momente (in realitate, o astfel de independenta este rar intâlnita); lantul Markov asociat starilor este omogen.
    Presupunând ca fiecare lovitura (atac) aeriana modifica starea marii unitati si ca inamicul aerian executa trei lovituri (atacuri) aeriene asupra marii unitati, respectiv asupra obiectivului de aparat impotriva actiunilor din aer si ca statul major doreste sa cunoasca vectorii probabilitatii de stare a sistemului dupa fiecare lovitura aeriana si având in vedere ca vectorul probabilitatilor de stare a sistemului pentru momentul "k" (P_k = {p_ki}, i = 1, ..., n; S p_ki =1) este egal cu produsul dintre vectorul probabilitatii de stare a sistemului pentru starea "k-1" si matricea densitatii probabilitatilor de trecere de la starea "k-1" la "k" (in cazul nostru aceasta este unica pentru toate starile), avem:

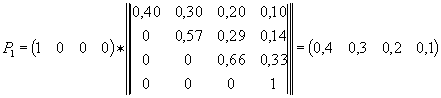
P1 = (0,40 0,30 0,20 0,10), care arata ca dupa primul atac aerian, sistemul are mari sanse sa se afle in starea S₁(40%) sau S₂(30%);

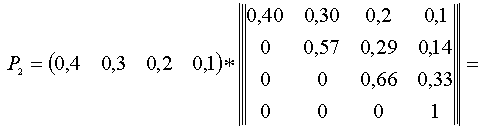(0,16 0,29 0,30 0,25)

P₂ = (0,16 0.29 0.30 0.25), de unde rezulta ca sistemul se va gasi in starea S₃ cu cea mai mare probabilitate (30%) sau, daca concluziile sunt mai prudente, in starea S₂(29%);

(0,064 0,21 0,314 0,41)

P 3 = (0,064 0,21 0,314 0,41).
    Ca urmare rezulta ca procedeul de actiune ales de comandamentul marii unitati de artilerie si rachete antiaeriene nu asigura indeplinirea misiunii de lupta, deoarece dupa cea de-a treia lovitura aeriana executata de catre adversarul aerian, probabilitatea ca marea unitate sa fie in starea S₄, deci nimicita, este foarte mare, de 41%.
    Având la baza aceste date, desi aproximative comandantul si statul major vor actiona fie pentru schimbarea conceptiei de indeplinire a misiunii de lupta, fie in sensul modificarii factorilor controlabili ce influenteaza matricea de trecere.
    Daca tinem seama de realitatea câmpului de lupta modern, in care se manifesta intens riscul si incertitudinea, atunci vectorul probabilitatilor de stare initiala (P₀) nu ar fi avut valorile (1 0 0 0), ce de fapt corespunde pentru situatia sigura, respectiv in conditii de certitudine, ci cu valori subunitare ale p_0i, având evident .

Bibliografie
[1] Cam.(r.) dr. Grad, V., colectiv, Cercetare operationala in domeniul militar, Editura Sylvi, Bucuresti, 2000.
[2] Boldur-Latescu, G., colectiv, Cercetare operationala cu aplicatii in economie, Editura Didactica si Pedagogica, Bucuresti, 1979.