Fiabilitatea este unul dintre domeniile cele mai dinamice ale stiintei si tehnicii contemporane, avand un impact major asupra cercetarii, proiectarii si producerii produselor industriale, precum si asupra serviciilor. Ca in orice domeniu dinamic apar continuu elemente noi care, uneori, necesita noi metode de abordare, folosind, de exemplu, teorii care pana nu demult erau strict legate de alte domenii. In lucrare vor fi prezentate pe scurt cateva notiuni ale unor teorii care au patruns recent in fiabilitate ca metode de studiu, in special, al fiabilitatii sistemelor. Acestea sunt: multimile fuzzy si retelele Petri.

2. Multimi fuzzy
Fie X o multime nevida numita multime universala sau univers.
Orice submultime A (in sens clasic) a lui X poate fi reprezentata in doua moduri: primul prin enumerarea elementelor sale si al doilea, analitic, prin functia sa caracteristica.
Functia caracteristica a unei submultimi A Í X este [ 2] :

. (1)

In consecinta, se poate spune ca multimea partilor lui X este in corespondenta bijectiva cu multimea functiilor f:X® {0,1}.
Submultimile fuzzy ale lui X sunt in corespondenta bijectiva cu multimea functiilor f:X® [0,1]. Aplicatia corespunzatoare f_F:X® [0,1] a unei submultimi fuzzy F a lui X se numeste functie de apartenenta a lui F[2] . In principiu, oricarei afirmatii cu caracter imprecis i se poate asocia o multime fuzzy.
Definitia 1.[ 1] Fie un univers X. Se numeste multime fuzzy a lui X, multimea de perechi ordonate

, (2)
unde :X® [0,1] este functia sa de apartenenta.
Pentru un element oarecare xÎ X,  reprezinta gradul de apartenenta [1] al elementului x la multimea fuzzy. . Spre deosebire de multimile clasice, unde elementele fie apartin fie nu apartin multimii respective, multimile fuzzy permit apartenenta partiala, gradul de apartenenta putand avea valori in intreg domeniul de la 0 (neapartenenta) pana la 1 (apartenenta totala).
Definitia 2.[1] Fie  o multime fuzzy a lui X. Suportul lui  este multimea:

S() = .

Operatiile uzuale din teoria clasica a multimilor (reuniune, intersectie, complementare) se pot defini si pentru multimile fuzzy. Definirea acestora nu este unica, dar o vom considera numai pe aceea sugerata de Zadeh. In continuare sunt prezentate doar acele operatii cu multimi fuzzy cu o mai mare utilizare in fiabilitate.
Definitia 3.[1] Functia de apartenenta  a intersectiei este definita punctual prin

= , xÎ X. (3)
Definitia 4.[1] Functia de apartenenta  a reuniunii este definita punctual prin

= , xÎ X. (4)
Definitia 5.[ 1] Functia de apartenenta a complementarei multimii fuzzy,  este definita punctual prin

, xÎ X. (5)

Definitia 6.[ 1] Suma algebrica (suma probabilistica)  se defineste ca

, (6)
unde
.
In teoria fiabilitatii literatura de specialitate mentioneaza mai multe domenii in care se folosesc multimile fuzzy si anume:
- analiza nivelului de performanta al sistemelor [3];
- analiza fiabilitatii sistemelor folosind arbori de evenimente si teoria multimilor fuzzy [4];
- selectarea strategiilor de mentenanta pentru sistemele cu mai multe stari [5];
- planificarea actiunilor de mentenanta [1];
- determinarea fiabilitatii utilizand interferenta discreta intre solicitare si rezistenta [6].

3. Retele Petri

Reteaua Petri simpla, ca reprezentare a unui sistem, se bazeaza pe doua concepte: tranzitiile si conditiile.
Tranzitiile sunt actiuni care au loc in sistem si a caror realizare este controlata prin starea sistemului.
Starea unui sistem poate fi descrisa ca o multime de conditii.
Conditia este o descriere logica a starii unui sistem.
Pentru ca o tranzitie sa se realizeze poate fi necesar ca anumite conditii sa fie indeplinite. Acestea sunt numite preconditii ale tranzitiei. Realizarea unei tranzitii poate determina incetarea indeplinirii unor preconditii si poate determina indeplinirea altor conditii, numite postconditii.
O retea Petri are nevoie pentru descriere de urmatoarele notiuni:

• pozitiile, folosite pentru reprezentarea conditiilor;
• tranzitiile, folosite pentru reprezentarea evenimentelor;
• intrarile – aplicatii de la tranzitii la pozitii;
• iesirile – aplicatii de la pozitii la tranzitii;
• marcajele, folosite pentru a atribui puncte pozitiilor;
• punctele, folosite la executia unei retele Petri.

• relatii explicite intre evenimente;
• existenta unui anumit limbaj ce poate descrie sistemul la diferite nivele de abstractizare;
• reprezentarea retelei permite examinarea proprietatilor sistemului si verificarea corectitudinii procesului.

PN = (P, T, F, W, M₀),
unde:
P = {p₁, p₂, ..., p_m} este multimea finita a pozitiilor;
T = {t₁, t₂, ..., t_n} este multimea finita a tranzitiilor;

FÍ (P´ T)? (T´ P) este multimea arcelor orientate;

W:F® N* este functia de ponderare a arcelor;

M₀:P® N este marcajul initial al retelei.
Pentru a simula evolutia unei retele este esentiala regula de executie a unei tranzitii [ 8] :
– o tranzitie t este executabila daca fiecare pozitie de intrare p are un marcaj cel putin egal cu ponderea arcului de la p la t, notata w(p, t);
– o tranzitie executabila poate sa fie sau nu executata;
– dupa executarea unei tranzitii t, fiecare pozitie de intrare p pierde w(p,t) puncte din marcaj, iar la fiecare pozitie de iesire (postconditie) p’ marcajul creste cu w(t, p’) puncte, care reprezinta capacitatea arcului de la tranzitia t la postconditia p’.
Pentru formalizarea acestor reguli [ 8] se utilizeaza descrierea retelelor Petri prin matricea de incidenta, [a_i,j], dim (A) = n´ m, ale carei elemente sunt numere intregi calculate astfel:

a_i,j =  – , (7)
unde:
este ponderea arcului de la tranzitia t_i la postconditia p_j;
este ponderea arcului de la preconditia p_j la tranzitia t_i.
Se observa ca ,  si a_i,j reprezinta numarul de puncte care parasesc, se adauga sau se schimba in pozitia p_j dupa executarea tranzitiei t_i.
Pentru un marcaj oarecare M_j, tranzitia t_i este executabila daca si numai daca:
? M_j, j = 1, 2, …, m. (8)
Considerand ca reteaua se gaseste in marcajul M_k–1 si tranzitia t_i este executabila, dupa executia ei noul marcaj al retelei M_k va fi dat de:
M_k = M_k–1 + coloana_i (A^T). (9)
Pe baza relatiilor (8) si (9) se poate construi graful de accesibilitate[8] al unei retele care cuprinde totalitatea marcajelor prin care poate sa treaca o retea; acesta se reprezinta ca un graf orientat ale carui noduri sunt marcajele posibile M₀, M₁, ..., iar arcele sunt orientate M_i – M_j si etichetate t_k daca pentru marcajul M_i tranzitia t_k este executabila, iar dupa executia ei reteaua capata marcajul M_j.
Pe baza grafului de accesibilitate se pot evidentia proprietatile comportamentale ale unei retele Petri. Acestea sunt: accesibilitatea, marginirea, viabilitatea, reversibilitatea si persistenta.
Definitia 8.[ 7] O retea Petri este ordinara daca toate arcele au pondere unitara.
Definitia 9.[ 7] O retea Petri cu arce inhibitoare este o retea extinsa printr-o functie speciala de incidenta F_I: P´ T® {0,1} care defineste arcele inhibitoare pentru toate perechile (p, t) pentru care F_I(p, t) = 1.
Un arc inhibitor pleaca dintr-o pozitie si soseste la o tranzitie. O tranzitie la care sosesc si arce inhibitoare pentru a putea fi executata, trebuie sa indeplineasca, pe langa conditia de executabilitate si urmatoarea conditie: pozitiile conectate prin arce inhibitoare la tranzitia respectiva trebuie sa nu aiba puncte. Acest tip de retea Petri creste puterea de modelare, facand din ea un echivalent al masinii Turing.
Tipuri de retele Petri stochastice
Este o subclasa speciala de retele care face parte din clasa retelelor Petri cu temporizare.
Se cunosc mai multe tipuri de retele Petri stochastice si anume:
– retele Petri stochastice (propriu-zise), SPN;
– retele Petri stochastice generalizate, GSPN;
– retele Petri temporizate stochastice, TSPN;
– retele stochastice cu compensare, SRN;
– retele Petri stochastice extinse, ESPN.
Retele Petri stochastice (SPN) [ 8]
Definitia 10. O retea Petri stochastica este reteaua Petri la care timpii de executie ai tranzitiilor retelei sunt distribuiti exponential.
Variabila timp se introduce astfel: din momentul in care t_i este executabila, un numar de  puncte ( este capacitatea (ponderea) arcului orientat de la preconditia p_j la tranzitia t_i) vor astepta in pozitia p_j timp de d_i unitati de timp inainte ca tranzitia sa fie efectiv executata. Pentru obtinerea unor modele consistente se presupune ca intarzierile d_i sunt variabile aleatoare avand o distributie exponentiala cu parametrul l_i:
F(d_i) = (10)
si deci valoarea mediei (statistice) intarzierii va fi:
E(d_i) =. (11)
Este evident faptul ca retelele Petri stochastice pot fi studiate prin acelasi formalism matematic ca si procesele Markov. Intr-adevar, reprezentarea grafica a unui proces Markov este izomorfa cu graful de accesibilitate al retelei, tinand seama de faptul ca starile procesului sunt reprezentate de multimea marcajelor retelei. Diferenta esentiala consta in faptul ca, spre deosebire de procesele Markov, in cazul retelelor Petri o tranzitie care a devenit executabila va fi in mod cert executata dupa un interval de timp egal cu intarzierea d_i aferenta ei. In aceasta situatie, probabilitatea de trecere de la starea (marcajul) i la starea (marcajul) j va fi q_i,j = 1, iar rata instantanee de tranzitie va capata forma:
a_i,j = l_iq_i,j = l_ij. (12)
Cu aceste observatii se poate prezenta procedura de analiza a retelelor Petri stochastice:[ 8]
a) se construieste graful de accesibilitate al retelei;
b) se construieste spatiul starilor (graful) pentru procesul Markov izomorf astfel: multimea starilor procesului (nodurile grafului) este identica cu graful de accesibilitate al retelei; arcele dintre doua noduri sunt ponderate cu l_i, parametrul temporal al tranzitiei a carei executie determina trecerea dintr-un marcaj intr-altul. Daca intre doua marcaje M_i si M_j sunt mai multe tranzitii executabile, atunci arcul corespunzator va fi ponderat cu suma parametrilor (ratelor) aferenti acestor tranzitii (proprietatea de aditivitate a repartitiei exponentiale);
c) se construieste matricea generatoare A (care nu trebuie confundata cu matricea de incidenta a retelei Petri) tinand seama de faptul ca elementele de pe diagonala principala trebuie alese astfel incat suma de pe fiecare linie a matricii A sa fie nula;
d) daca reteaua este reversibila, atunci procesul Markov asociat este omogen si ireductibil. Daca si multimea starilor procesului (respectiv multimea marcajelor accesibile) este finita, atunci procesul este recurent nenul. In aceasta situatie, sistemul de ecuatii:
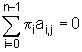; j = 1, 2, ..., n

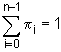, (13)

unde n este numarul marcajelor accesibile, are o solutie unica. Aceasta este distributia stationara, iar p_i reprezinta probabilitatea ca reteaua sa fie in marcajul M_i;
e) deoarece numarul de puncte in fiecare pozitie este o variabila aleatoare, se poate calcula media ei (statistica) cu formula cunoscuta pentru variabile discrete:

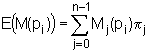, (14)

unde s-a notat cu M(p_i) numarul de puncte din pozitia p_i in cadrul marcajului M_j;
f) se determina numarul mediu de tranzitii in unitatea de timp (frecventa de executie a tranzitiei t_j, sau probabilitatea executiei acestei tranzitii) cu relatia:

f_j = 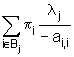, (15)

unde B_j reprezinta submultimea marcajelor din care t_j este executabila.

Retele Petri stochastice generalizate (GSPN) [9]
GSPN-urile sunt retele Petri care imbina SPN-urile cu retelele Petri clasice. Astfel, intr-o GSPN se intalnesc atat tranzitii imediate cat si tranzitii temporizate, avand timpi de executie distribuiti exponential.
Intr-o GSPN exista doua tipuri de marcaje: marcaje pe cale de disparitie daca exista cel putin o tranzitie imediata executabila si marcaje tangibile, in caz contrar.
Ciardo si altii [9] au introdus cateva extensii ale GSPN-urilor, ca de exemplu:
– functii de validare pentru tranzitii (tranzitiile sunt validate pe baza unor conditii stabilite explicit si nu numai pe baza distributiei punctelor in pozitiile de intrare);
– multiplicitati de arc dependente de marcaj;
– prioritati ale tranzitiilor temporizate;
– arce inhibitoare.
O GSPN poate fi convertita usor intr-un lant Markov.
Retele Petri temporizate stochastice (TSPN) [10]
TSPN-urile sunt retelele Petri care, pe langa atributele unei retele Petri propriu-zise, poseda:
– o functie interval de executie, care face ca fiecarei tranzitii t_i sa i se asocieze un interval de executie I_i = [A_i, B_i], cu 0 ? A_i ? B_i, A_i si B_i fiind limita inferioara, respectiv limita superioara a intervalului de timp in care tranzitia este executabila;
– o functie densitate de probabilitate de trecere, care face ca fiecarui interval I_i sa i se asocieze o densitate de probabilitate f_i(x) (care poate avea orice forma), cu:

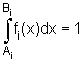. (15)

Retele stochastice cu compensare (SRN) [9]
SRN-urile difera de GSPN-uri prin faptul ca poseda rate de compensare (valori numerice) care sunt specificabile la nivelul retelei si transpuse intr-o rata de compensare asociata cu fiecare marcaj al retelei. Folosirea ratelor de compensare reduce dimensiunea retelei deoarece multe aspecte ale sistemului, care ar putea fi modelate explicit prin pozitii si tranzitii intr-o GSPN, pot fi exprimate prin expresii aritmetice si booleene in cadrul ratelor de compensare intr-o SRN.
Retele Petri stochastice extinse (ESPN) [11]
ESPN-urile contin tranzitii ale caror intarzieri pot fi deterministe sau stochastice cu o distributie generalizata, cu conditia ca aceste tranzitii sa fie neconcurente.
Pentru tranzitiile concurente se foloseste distributia exponentiala. Modelele de baza ale acestor retele sunt procesele semi-Markov. Doua tranzitii se numesc concurente in marcajul M daca si numai daca executarea fiecareia nu atrage dupa sine invalidarea celeilalte.
Utilizarea in fiabilitate a retelelor Petri stohastice este din ce in ce mai extinsa. Tinand cont ca un proces de defectare poate fi considerat ca un proces discret de trecere de la starea de buna functionare la starea de defectare, modelarea cu retele petri a proceselor complexe de defectare a sistemelor, ca urmare a defectarii componentelor sale, este in multe cazuri salutara datorita faptului sunt extrem de versatile si, in acelasi timp, intuitive. Tinand cont de izomorfismul acestui tip de retele cu procesele Markov, constructia acestora se va face simplu, folosindu-se graful de accesibilitate, iar odata cunoscut procesul Markov rezolvarea problemei se va face cu metodele specifice acestui tip de proces.

1. Zimmermann, H.J. – Fuzzy Set Theory and its Applications, second edition, Kluwer Academic Publishers, 1991.
2. Negoita, C., Ralescu, D.A. – Multimi vagi si aplicatiile lor, Editura Tehnica, Bucuresti, 1974.
3. Tarcolea, C., Filipoiu, A., Bontas, S. – Tehnici actuale in teoria fiabilitatii, Editura ªtiintifica si Enciclopedica, Bucuresti, 1989.
4. Kenarangui, R. – Event Tree Analysis by Fuzzy Probability, IEEE Transactions on Reliability, vol. 40, No. 1., 1991 aprilie.
5. Suresh, P. V., Chaudhuri, D., Rao, B.V.A. – Fuzzy Set Approach to Select Maintenance Strategies for Multistate Equipment, IEEE Transactions on Reliability, vol. 43, No. 3, 1994 septembrie.
6. Wang, J. D., Liu, T. S. – Fuzzy Reliability Using a Discrete Stress-Strength Interference Model, IEEE Transactions on Reliability, vol.45, No. 1., martie, 1996.
7. Banaszak, Z. – Modelling and Control of FMS. Petri Net Approach, Wroclaw Tehnical University Press, 1991.
8. Russ, I., Tabus, I., Dumitrescu, B., Petre, D. – Modelare si simulare. Indrumar de lucrari practice, Universitatea „Politehnic" Bucuresti, Fac. de Automatica si Calculatoare, Catedra Calculatoare de Proces si Automatizari, 1994.
9. Malhotra, M., Trivedi, K.S. – Dependability Modeling Using Petri Nets, IEEE Transactions on Reliability, vol. 44, No. 3, septembrie 1995.
10. Desmas, Th., Ancelin, C., Villmeur, A. – Les méthodes de la fiabilité et la s?reté de fonctionnement, Revue générale d’électricité, No. 8/92, septembrie 1992.
11. Guo, D. L., DiCesare, F., Zhon, M. C. – A Moment Generating Function Based Approach for Evaluating Extended Stochastic Petri Nets, IEEE Transaction on Automatic Control, vol. 38, No. 2, februarie, 1993.

                                                                            Inapoi la cuprins