Fie ecuatia integrala
unde
Un prim rezultat cu privire la existenta solutiilor pentru ecuatia (2.1) poate fi obtinut prin metoda aproximatiilor succesive:
Teorema 1. Ecuatia (2.1) admite o unica solutie continua pe [ a,b] daca are loc:
Lt.col.prof.mil. Alexandru Hampu
2. Consideratii generale
Fie ecuatia integrala
![]() (2.1)
(2.1)
unde ![]() si
si ![]() sunt cunoscute.
sunt cunoscute.
Un prim rezultat cu privire la existenta
solutiilor pentru ecuatia (2.1) poate fi obtinut prin metoda aproximatiilor
succesive:
Teorema 1. Ecuatia (2.1) admite
o unica solutie continua pe [ a,b] daca are loc:
![]() ,
(2.2)
,
(2.2)
unde ![]() .
.
In demonstratia acestei teoreme
apare o functie importanta:
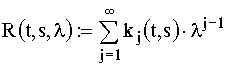 ,
(2.3)
,
(2.3)
unde ![]()
iar ![]() ,
,
care se numeste nucleu rezolvent
asociat lui k.
Nucleul k si nucleul rezolvent R
sunt legate prin urmatoarele ecuatii:
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
Rolul insemnat al ecuatiilor (2.4)
si (2.5) reiese din urmatoarea
Teorema 2. Sa presupunem ca exista
o functie R pentru un l dat (nu obligatoriu satisfacand (2.2)) continua
pentru (t, s)![]() astfel incat
sa verifice (2.4) si (2.5). atunci ecuatia (2.1) are o mica solutie pentru
acea valoare a lui l si ea este data de:
astfel incat
sa verifice (2.4) si (2.5). atunci ecuatia (2.1) are o mica solutie pentru
acea valoare a lui l si ea este data de:
![]() (2.6)
(2.6)
3. Metoda ecuatiei perturbate
Evident ca nu putem gasi nucleul
rezolvent pentru orice ecuatie integrala liniara de tip Fredholm. Ideea
este de a „atasa" ecuatiei integrale date o ecuatie integrala al carei
nucleu rezolvent sa il putem gasi si a carei solutie sa se „apropie" oricat
de mult de solutia ecuatiei date.
Fie ecuatia integrala:
![]() (3.1)
(3.1)
si ecuatia „perturbata"
![]() (3.2), unde
(3.2), unde ![]() poate fi eventual
degenerat, iar f,
poate fi eventual
degenerat, iar f, ![]() , si
, si ![]() ,
,![]() .
.
Teorema 3. Daca urmatoarele conditii
sunt indeplinite
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
unde:
![]() e nucleul rezolvant al lui
e nucleul rezolvant al lui ![]() ,
,
![]() (3.5)
(3.5)
si
![]() (3.6)
(3.6)
atunci are loc inegalitatea
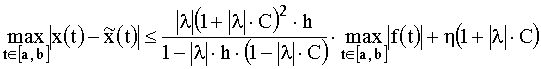 .
.
Altfel spus, daca ![]() este „aproape" si
este „aproape" si ![]() este
„aproape" de K, atunci si
este
„aproape" de K, atunci si ![]() se „apropie" de x (respectandu-se relatiile (3.4) si (3.6)).
se „apropie" de x (respectandu-se relatiile (3.4) si (3.6)).
Vom da in continuare un exemplu
de rezolvare a unei ecuatii integrale liniare de tip Fredholm cu nucleul
degenerat prin metoda ecuatiei perturbate (ecuatia perturbata fiind chiar
ea).
Fie ecuatia:
![]() (3.7)
(3.7)
Nucleul este:
![]()
Vom cauta nucleul rezolvent R asociat
lui K.
Avem:
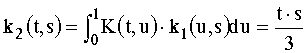
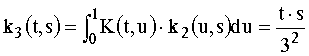
Prin inductie se poate demonstra
ca:
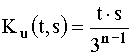
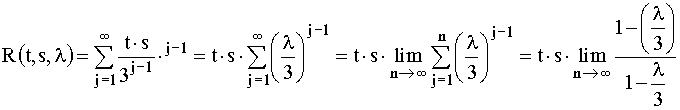
Daca ![]() ,
atunci
,
atunci  ,
,
adica 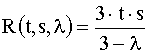
Avand in vedere teorema 2 putem scrie:
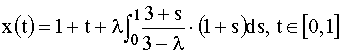 .
.
Efectuand calculele obtinute:
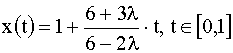
Bibliografie
1. Munteanu I. – Analiza functionala.
Capitole speciale, Universitatea „Babes-Bolyai", Cluj-Napoca, 1990.
2. Munteanu I. – Analiza functionala,
Universitatea „Babes-Bolyai", Cluj-Napoca, 1993.
3. Scheiber E. – Analiza numerica.
Curs si culegere de probleme, vol. II, Universitatea din Brasov, 1985.