CERCETAREA
OPERATIONALA
SI DOMENIUL MILITAR
Lt.col.prof.mil. Alexandru
Hampu
Cpt.asist.univ. Vasile Carutasu
Cercetarea operationala este o ramura
a matematicii aplicate aparuta de cateva decenii (in anii 40) si se ocupa
de stabilirea solutiilor optime in cazul proceselor, fenomenelor in care
se impune luarea unei decizii. Este de altfel denumita stiinta optimizarii
deciziilor.
Ca stiinta integratoare se bazeaza
pe alte ramuri ale matematicii (algebra, analiza, matematica, probabilitati
etc.), dar s-a structurat in forma oarecum asemanatoare celei cunoscuta
astazi inaintea celui de-al doilea razboi mondial si a fost utilizata de
S.U.A. si Anglia pentru stabilirea cursului optim al actiunilor militare,
de unde si denumirea de cercetare operationala.
Prin urmare aceasta stiinta este
nascuta din ratiuni militare, aplicabilitatea ei este certa, verificata
in numeroase actiuni militare si avantajele aduse de utilizarea ei a determinat
preluarea si de catre alte domenii a metodelor acesteia, de exemplu in
economie, industrie, agricultura, domeniul social etc.
Caracterul pur militar al acestei
discipline este reliefat si de notiunile cu care se opereaza si astazi,
chiar daca aplicabilitatea ei este si in domeniul civil si anume: operatie,
parte operativa, strategie a partii operative, functie obiectiv, conflict
etc.
Care sunt principalele capitole
ale cercetarii operationale?
Dintre cele mai importante reamintim
urmatoarele:
1. Teoria problemelor de optimizare
cu restrictii (programarea matematica) care se ocupa de optimizarea unor
criterii (functii obiectiv) avand anumite restrictii (de timp, financiare
etc.).
2. Teoria jocurilor analizeaza conflictele
dintre doi sau mai multi adversari si permite stabilirea strategiei optime
a fiecaruia.
3. Teoria grafurilor studiaza alegerea
deciziei optime in probleme care se pot reprezenta prin anumite scheme
numite grafuri.
4. Teoria stocurilor stabileste
dimensiunea optima a unei acumulari de resurse.
5. Teoria echipamentelor studiaza
modul optim de inlocuire a echipamentelor datorita uzurii fizice si morale.
6. Teoria fenomenelor de asteptare
studiaza acele procese unde pentru efectuarea unei operatii se produc aglomerari.
Toate aceste capitole opereaza cu
modele matematice specifice acestei discipline la a caror realizare trebuie
de regula sa colaboreze specialisti militari, matematicieni, informaticieni.
Dupa crearea modelului in majoritatea situatiilor se intocmesc programe
pe calculator care permit utilizarea simpla si rapida a acestora in diferite
situatii.
Vom da doua exemple prin care se
poate observa ca daca incercam sa tratam empiric o problema decizionala
sansele de gasire a solutiei optime sunt minime, pe cand folosirea acestor
metode specifice cercetarii operationale ne dau solutia optima.
Primul exemplu este specific programarii
matematice liniare (sau optimizarii liniare) si poate fi aplicat in stabilirea
repartitiei mijloacelor de foc pe obiective.
Exemplul 1
Asupra doua tipuri de lucrari de
aparare O1 si O2 se trage cu 3 tipuri de lovituri
de artilerie L1, L2, L3 pentru a fi distruse.
Numarul loviturilor existente este de 20, 30, 40. Cunoscand ca distrugerea
unui obiectiv O1 produce inamicului pierderi de 3%, iar a unui
obiectiv O2 de 5% numarul loviturilor necesare distrugerii fiind
date in tabel se cere sa se stabileasca cate obiective O1 respectiv
O2 vor fi distruse astfel incat pierderile sa fie maxime.
| |
O1
|
O2
|
Nr. lov. existente
|
|
L1
|
2
|
4
|
20
|
|
L2
|
3
|
3
|
30
|
|
L3
|
5
|
6
|
40
|
|
Pierderi
|
3%
|
5%
|
|
Rezolvare:
3x1+5x2®max
(1)
cu restrictiile:
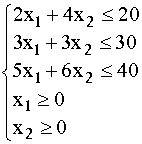 (2)
(2)
unde am notat cu x1 si
x2 numarul obiectivelor O1 respectiv O2.
Rezolvarea acestei probleme se face
prin algoritmul simplex primal solutia gasita fiind urmatoarea.
Solutia optima deci este 5 obiective
O1, 2,5 obiective O2 (in cazul cand se poate distruge
partial un obiectiv O2) pierderile produse fiind de 27,5%.
Este singura posibilitate de a alege
numarul obiectivelor ce vor fi distruse astfel incat sa fie respectate
restrictiile problemei (2) si criteriul ales (pierderi maxime) sa fie realizat.
Alegerea oricarui alte variante este mai proasta decat aceasta.
Un alt exemplu care poate fi tratat
prin teoria jocurilor si se rezolva printr-un algoritm specific.
Exemplul 2
O unitate de geniu trebuie sa amplaseze
un camp de mine pe directia de actiune a unei unitati de tancuri: unitatea
de geniu poate organiza 3 tipuri de campuri de mine antitanc C1,
C2, C3 iar unitatea de tancuri are la dispozitie
3 variante de actiune V1, V2, V3. Pentru
fiecare tip de camp de mine pierderile in tancuri pentru o anumita varianta
de actiune este dat in tabelul de mai jos. Sa se stabileasca modul optim
de actiune a unitatii de geniu astfel incat numarul tancurilor distruse
sa fie maxim.
| |
V1
|
V2
|
V3
|
|
C1
|
2
|
0
|
3
|
|
C2
|
0
|
5
|
1
|
|
C3
|
4
|
3
|
2
|
Rezolvand acest joc printr-una din
metodele cunoscute (matriceala) se obtine rezultatul: trebuie instalat
campul de mine C1 in proportie de 3/7 si campul de mine C3
in proportie de 4/7 pentru a avea un castig de 2,57 adica 2-3 tancuri distruse,
cu certitudine, indiferent de varianta utilizata de adversar.
Am prezentat deci doua exemple de
utilizare a cercetarii operationale in aplicatii cu caracter militar in
vederea optimizarii deciziilor.
Folosirea acestor metode permite
adoptarea unor hotarari cu probabilitatea de a prevedea care sunt rezultatele
posibile asteptate; chiar in cazuri de totala incertitudine exista procedee
de stabilire a strategiei optime (optimizare stocastica, jocuri stocastice
etc.).
Se impune ca viitorii ofiteri sa
cunoasca in primul rand ce se poate realiza prin aceste metode, care sunt
avantajele pe care le aduce o astfel de abordare. In contextul general
al managementului modern, al actiunii eficiente, optime, la orice nivel
important este sa stim sa folosim acest mecanism, sa exploatam la maximum
posibilitatile puse la dispozitie de metodele de optimizare.
Urmatorul pas absolut necesar va
fi realizarea de programe pentru toate aceste metode (multe dintre ele
exista) si antrenarea ofiterilor in utilizarea lor pe scara larga, in diferite
actiuni decizionale in asa fel incat rezultatul obtinut sa fie optim.
Inapoi la cuprins
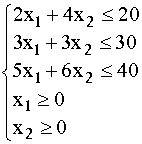 (2)
(2)